동적 계획법(Dynamic Programming, DP)은 알고리즘이라기 보다는 하나의 기술이다.
분할 정복에서 사용하는 기법으로, 큰 문제들을 작은 문제들로 쪼개서 그 답을 저장하고 재활용한다.
쉽게 말하자면 '기억하며 풀기' 라고 할 수 있다.
왜 DP를 사용하는가?
다음과 같은 함수를 계산한다고 해보자.
- $f(a, b) = f(a-1, b)+f(a, b-1)\space(a, b\ge 1)$
- $f(0, n)=f(n, 0)=1$
이떄 f(2, 2)를 계산한다고 하면 다음과 같은 계산 과정를 거치게 된다.
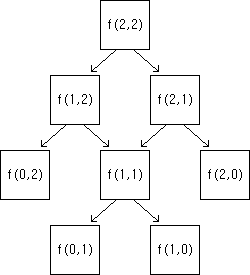
위 에서는 총 5번의 연산을 수행하는데, 이때 f(1, 1)에 대한 연산을 2번 수행하고 있으므로 이를 미리 연산한다고 가정하면 f(2, 2)를 구하기 위해 4번의 연산만 수행하면 된다. 만약 a, b의 값이 커진다면 속도면에서 다음과 같이 큰 이득을 볼 수 있다.
| (a, b) | 일반적으로 계산시 | 동적 계획법 이용시 연산 횟수 |
| (2, 2) | 5 | 4 |
| (4, 4) | 69 | 16 |
| (6, 8) | 3002 | 48 |
| (10, 10) | 184755 | 100 |
즉, DP를 사용하면 재귀함수에서 기하급수적으로 증가하는 중복되는 연산량을 매우 효과적으로 줄일 수 있다.
DP로 문제 풀기
일반적으로 DP를 사용하기 전에는 다음과 같은 과정을 거쳐 진행한다.
- DP로 풀 수 있는 문제인지 확인한다
- Overlapping Subproblems (겹치는 부분 문제)
동일한 작은 문제들이 반복해서 나타나는 경우에 사용가능하다. - Optimal Substructure (최적 부분 구조)
부분 문제의 최적 결과 값을 통해 전체 문제의 최적 결과를 낼 수 있는 경우에 사용가능하다.
- Overlapping Subproblems (겹치는 부분 문제)
- 문제의 변수를 파악한다
- 점화식을 만든다 : 문제간의 점화식을 설계한다.
- 메모이제이션 또는 타불레이션 : 문제의 답을 배열 등에 저장한다
- 기저 상태 파악하기 : 쉬운 문제의 조건과 답을 만든다
- 구현하기
참고 자료
https://hongjw1938.tistory.com/47
알고리즘 - Dynamic Programming(동적 계획법)
1. 개요 DP, 즉 다이나믹 프로그래밍(또는 동적 계획법)은 기본적인 아이디어로 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 것으로
hongjw1938.tistory.com
https://namu.wiki/w/%EB%8F%99%EC%A0%81%20%EA%B3%84%ED%9A%8D%EB%B2%95
동적 계획법 - 나무위키
동적 계획법의 개념과 구현에 대해 정확하게 짚고 넘어가기 위해 동적 계획법을 적용시킬 수 있는 예에 대해 알아보자. f(a,b) = f(a-1,b) + f(a,b-1) (a,b >= 1 )f(0,0) = 1, 임의의 자연수 n에 대해 f(n,0) = f(0,
namu.wiki
'알고리즘' 카테고리의 다른 글
| [알고리즘] 최장 증가 부분 수열(LIS) 알고리즘 (1) | 2023.05.20 |
|---|---|
| [알고리즘] 깊이 우선 탐색(DFS) / 너비 우선 탐색(BFS) (0) | 2023.05.16 |
