1. 등장 배경
a. 장기 의존 관계 학습의 어려움
RNN은 순환 경로를 포함하여 과거의 정보를 기억하고 현재 시점의 출력에 활용 할 수 있다. RNN은 단순한 구조를 가지고 있으나, 시계열 데이터에서 시간적으로 많이 떨어진 장기 의존 관계를 잘 학습하지 못하여 성능 문제가 있었다.
b. Vanishing Gradient BPTT
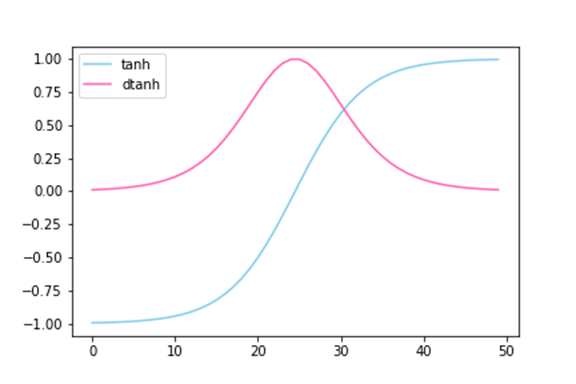
RNN 계층에서는 보통 $\tanh$를 활성화 함수로 활용하는데, 이때 gradient인 $(\tanh)`$는 항상 0~1 사이의 값을 가진다. 즉, 역전파에서 출력값은 노드를 지날 때 마다 값이 작아질 수 밖에 없다. 이로 인해 RNN 계층이 길어지게 되면 Vanishing Gradient가 발생한다.
2. Structure of LSTM
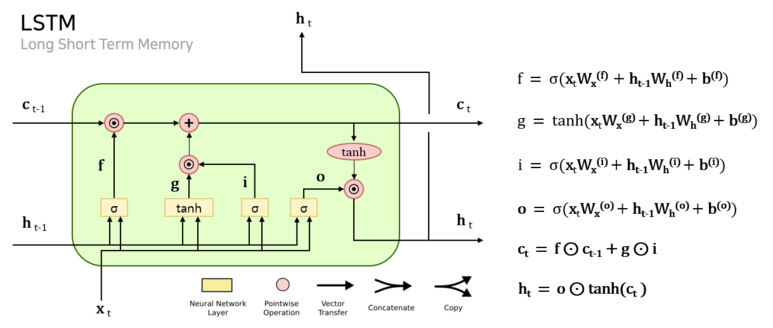
LSTM에는 RNN과 달리 기억 셀 $c_t$를 지니고 있다. $c_t$에는 시각 t에서의 LSTM의 메모리가 저장되어 있는데, 여기에는 과거에서 시각 t까지의 메모리가 저장되어 있다. LSTM은 3개의 입력 $(x_{t-1}, h_{t-1}, c_{t-1})$를 이용하여 구한 $c_t$를 사용해 $h_t$를 계산한다.
즉, LSTM 구조의 핵심은 Short Term Memory 인 $h_t$와 Long Term Memory in $c_t$라 할 수 있다.
3. Gate
LSTM에서 게이트는 데이터의 흐름을 어느정도 여닫을지 0~1 사이의 실수로 조절할 수 있다.
a. Output Gate
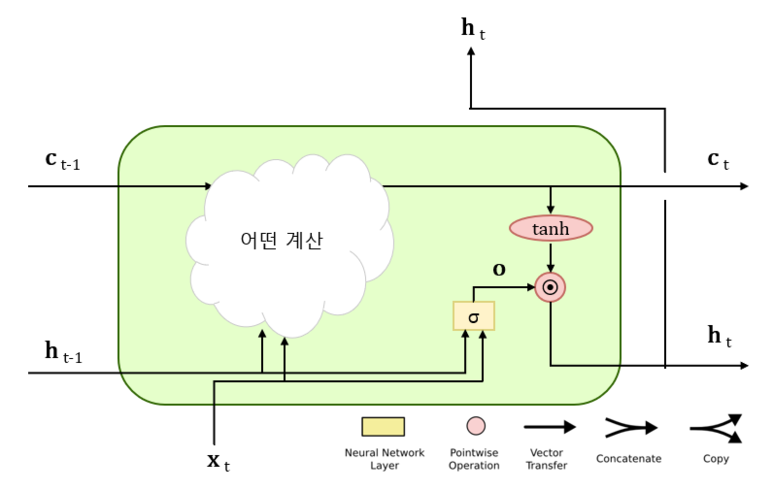
$o=\sigma (x_tW_x+h_{t-1}W_h+b)$로 표현된다. 여기서 $h_t=o\odot \tanh (c_t)$와 같이 계산된다.
b. Forget Gate
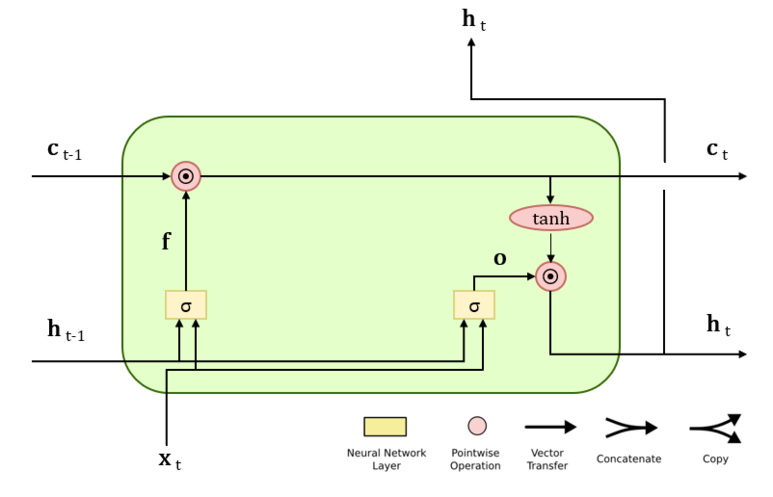
LSTM에서는 굳이 필요없는 정보를 계속 들고갈 필요는 없으므로 기억셀에 어떠한 정보를 잊을지 지시하는 게이트인 Forget Gate도 사용된다.
여기서도 Output Gate와 비슷하게 $f=\sigma (x_tW_x^{(f)}+h_{t-1}W_h^{(f)}+b)$와 같이 계산한다. 마찬가지로 $c_t=c_{t-1}\odot f$로 계산된다.
c. Update Gate
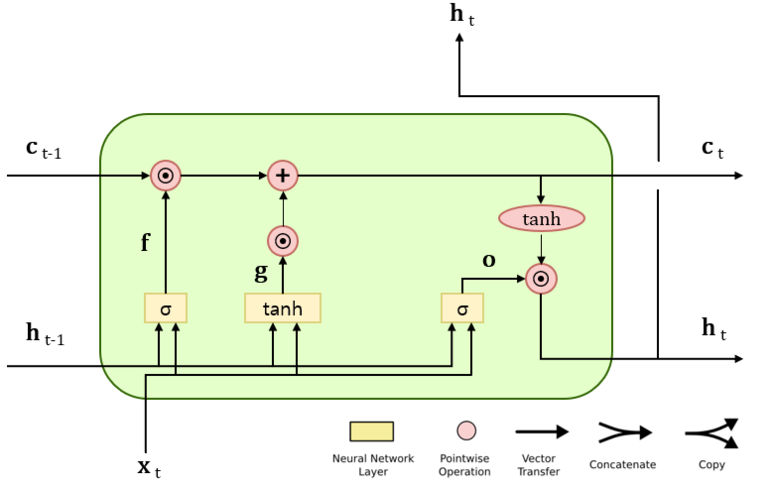
Forget Gate를 거치면서 이전 시각의 기억 셀로부터 잊어야 할 기억이 삭제되었으므로, 이제는 새로 들어온 데이터로 부터 새로운 정보를 추가해야한다. 이를 위해 $\tanh$노드를 추가하여 $g=tanh(x_tW_x^{(g)}+h_{t-1}W_h^{(g)}+b^{(g)})$와 같이 계산한다.
d. Input Gate
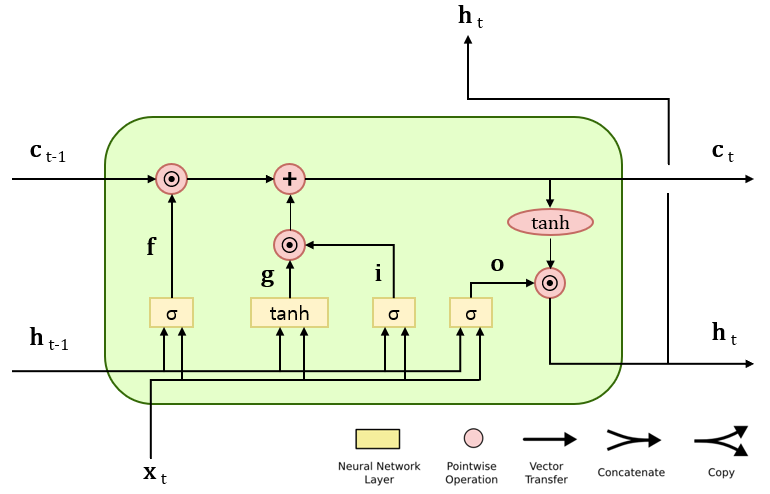
새로운 정보가 들어있는 g에 게이트를 추가하여 데이터를 얼마나 많이 반영할지 판단한다. $i=\sigma (x_tW_x^{(i)}+h_{t-1}W_h^{(i)}+b^{(i)})$와 같이 계산한다.
4. LSTM의 Gradient

기억셀의 역전파는 위의 그림에서 보이듯 $+$와 $\odot$ 노드만을 지나게 된다. + 노드는 Gradient를 그대로 흘릴 뿐 이므로 $\odot$ 에 집중해보자.
LSTM은 RNN과 달리 행렬곱이 아닌 아다마르 곱을 게산한다. 그리고 RNN과 같이 똑같은 가중치 행렬을 사용하는 것이 아닌, 새로 들어온 데이터에 대해서 행렬곱을 수행하게 된다. 그러므로 매번 새로운 값과 행렬곱이 되므로 곱셈의 효과가 누적되지 않아 Vanishing Gradient가 잃어나기 어려운 구조이다.
또한 $\odot$ 노드의 계산에 Forget Gate가 관여하는데, 역전파 계산시 Forget Gate의 출력과 상류 Gradient의 곱이 계산되므로, Forget Gate가 잊어야 한다고 판단한 기억 셀의 원소에 대해서는 해당 기울기가 작아지고, 잊어서는 안된다고 판단한 원소에 대해서는 그 기울기가 약화되지 않은 채로 과거 방향으로 전해진다.
Reference
'인공지능' 카테고리의 다른 글
| [인공지능] Recurrent Neural Network(RNN) (0) | 2023.07.03 |
|---|---|
| [인공지능] 머신러닝 (Machine Learning)이란 무엇인가 (0) | 2023.05.22 |
1. 등장 배경
a. 장기 의존 관계 학습의 어려움
RNN은 순환 경로를 포함하여 과거의 정보를 기억하고 현재 시점의 출력에 활용 할 수 있다. RNN은 단순한 구조를 가지고 있으나, 시계열 데이터에서 시간적으로 많이 떨어진 장기 의존 관계를 잘 학습하지 못하여 성능 문제가 있었다.
b. Vanishing Gradient BPTT

RNN 계층에서는 보통 $\tanh$를 활성화 함수로 활용하는데, 이때 gradient인 $(\tanh)`$는 항상 0~1 사이의 값을 가진다. 즉, 역전파에서 출력값은 노드를 지날 때 마다 값이 작아질 수 밖에 없다. 이로 인해 RNN 계층이 길어지게 되면 Vanishing Gradient가 발생한다.
2. Structure of LSTM

LSTM에는 RNN과 달리 기억 셀 $c_t$를 지니고 있다. $c_t$에는 시각 t에서의 LSTM의 메모리가 저장되어 있는데, 여기에는 과거에서 시각 t까지의 메모리가 저장되어 있다. LSTM은 3개의 입력 $(x_{t-1}, h_{t-1}, c_{t-1})$를 이용하여 구한 $c_t$를 사용해 $h_t$를 계산한다.
즉, LSTM 구조의 핵심은 Short Term Memory 인 $h_t$와 Long Term Memory in $c_t$라 할 수 있다.
3. Gate
LSTM에서 게이트는 데이터의 흐름을 어느정도 여닫을지 0~1 사이의 실수로 조절할 수 있다.
a. Output Gate

$o=\sigma (x_tW_x+h_{t-1}W_h+b)$로 표현된다. 여기서 $h_t=o\odot \tanh (c_t)$와 같이 계산된다.
b. Forget Gate

LSTM에서는 굳이 필요없는 정보를 계속 들고갈 필요는 없으므로 기억셀에 어떠한 정보를 잊을지 지시하는 게이트인 Forget Gate도 사용된다.
여기서도 Output Gate와 비슷하게 $f=\sigma (x_tW_x^{(f)}+h_{t-1}W_h^{(f)}+b)$와 같이 계산한다. 마찬가지로 $c_t=c_{t-1}\odot f$로 계산된다.
c. Update Gate

Forget Gate를 거치면서 이전 시각의 기억 셀로부터 잊어야 할 기억이 삭제되었으므로, 이제는 새로 들어온 데이터로 부터 새로운 정보를 추가해야한다. 이를 위해 $\tanh$노드를 추가하여 $g=tanh(x_tW_x^{(g)}+h_{t-1}W_h^{(g)}+b^{(g)})$와 같이 계산한다.
d. Input Gate

새로운 정보가 들어있는 g에 게이트를 추가하여 데이터를 얼마나 많이 반영할지 판단한다. $i=\sigma (x_tW_x^{(i)}+h_{t-1}W_h^{(i)}+b^{(i)})$와 같이 계산한다.
4. LSTM의 Gradient

기억셀의 역전파는 위의 그림에서 보이듯 $+$와 $\odot$ 노드만을 지나게 된다. + 노드는 Gradient를 그대로 흘릴 뿐 이므로 $\odot$ 에 집중해보자.
LSTM은 RNN과 달리 행렬곱이 아닌 아다마르 곱을 게산한다. 그리고 RNN과 같이 똑같은 가중치 행렬을 사용하는 것이 아닌, 새로 들어온 데이터에 대해서 행렬곱을 수행하게 된다. 그러므로 매번 새로운 값과 행렬곱이 되므로 곱셈의 효과가 누적되지 않아 Vanishing Gradient가 잃어나기 어려운 구조이다.
또한 $\odot$ 노드의 계산에 Forget Gate가 관여하는데, 역전파 계산시 Forget Gate의 출력과 상류 Gradient의 곱이 계산되므로, Forget Gate가 잊어야 한다고 판단한 기억 셀의 원소에 대해서는 해당 기울기가 작아지고, 잊어서는 안된다고 판단한 원소에 대해서는 그 기울기가 약화되지 않은 채로 과거 방향으로 전해진다.
Reference
'인공지능' 카테고리의 다른 글
| [인공지능] Recurrent Neural Network(RNN) (0) | 2023.07.03 |
|---|---|
| [인공지능] 머신러닝 (Machine Learning)이란 무엇인가 (0) | 2023.05.22 |
